Erdős-Rényi 图

本示例演示如何使用 Erdős–Rényi 图生成 igraph.GraphBase.Erdos_Renyi()。图有两种变体：

• Erdos_Renyi(n, p) 将从所谓的 \(G(n,p)\) 模型生成一个图，其中任意两对节点之间的每条边都以独立的概率 p 存在。

• Erdos_Renyi(n, m) 将从所有具有 n 个节点和 m 条边的图中均匀随机选择一个图。这被称为 \(G(n,m)\) 模型。

我们每种生成两个图，以便确认我们的图生成器是真正随机的。

import igraph as ig
import matplotlib.pyplot as plt
import random

首先，我们设置一个随机种子以实现可重现性。

random.seed(0)

然后，我们生成两个参数相同的 \(G(n,p)\) Erdős–Rényi 图。

g1 = ig.Graph.Erdos_Renyi(n=15, p=0.2, directed=False, loops=False)
g2 = ig.Graph.Erdos_Renyi(n=15, p=0.2, directed=False, loops=False)

为了进行比较，我们还生成了两个具有固定边数的 \(G(n,m)\) Erdős–Rényi 图。

g3 = ig.Graph.Erdos_Renyi(n=20, m=35, directed=False, loops=False)
g4 = ig.Graph.Erdos_Renyi(n=20, m=35, directed=False, loops=False)

我们可以打印出每个图的摘要以验证其随机性。

ig.summary(g1)
ig.summary(g2)
ig.summary(g3)
ig.summary(g4)

# IGRAPH U--- 15 18 --
# IGRAPH U--- 15 21 --
# IGRAPH U--- 20 35 --
# IGRAPH U--- 20 35 --

IGRAPH U--- 15 23 --
IGRAPH U--- 15 28 --
IGRAPH U--- 20 35 --
IGRAPH U--- 20 35 --

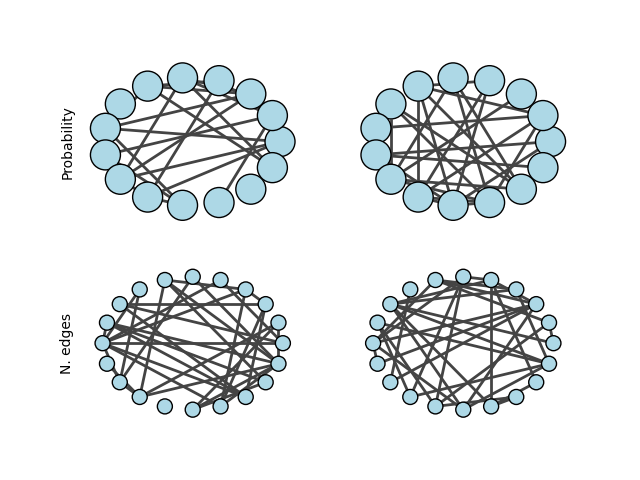
最后，我们可以绘制这些图以说明它们的结构和差异。

fig, axs = plt.subplots(2, 2)
# Probability
ig.plot(
    g1,
    target=axs[0, 0],
    layout="circle",
    vertex_color="lightblue"
)
ig.plot(
    g2,
    target=axs[0, 1],
    layout="circle",
    vertex_color="lightblue"
)
axs[0, 0].set_ylabel('Probability')
# N edges
ig.plot(
    g3,
    target=axs[1, 0],
    layout="circle",
    vertex_color="lightblue",
    vertex_size=15
)
ig.plot(
    g4,
    target=axs[1, 1],
    layout="circle",
    vertex_color="lightblue",
    vertex_size=15
)
axs[1, 0].set_ylabel('N. edges')
plt.show()